Was ist der beste Weg, um Ihre Schuhe zu binden? Physik kann die Antwort haben.

Der häufigste Fehler bei Ihrem Schnürsenkel binden macht versehentlich einen schwächeren Oma Knoten anstelle von den stärkeren Kreuzknoten. Jetzt kann Physik helfen Sie den perfekten Knoten zu binden, der egal was dicht bleibt.

Zwar ist es bekannt, dass alle die Knotenfestigkeit hängt von der Konfiguration, niemand versteht wirklich, konkret, warum dies sein sollte der Fall. Mit einem jüngst veröffentlichten Papier in Physical Review Lettershat ein Team von Physikern genommen einen wichtigen Schritt nach vorn in Entwirrung dieses Geheimnis, einkochen es alle zu einer einzigen Gleichung, die die Stärke und die Form von einem einfachen Knoten vorhersagt.

Knoten sind seit langem ein Schwerpunkt der Studie für Mathematiker in der abstrakten, aber Modellierung ihrer physikalischen Eigenschaften in der realen Welt ist bekanntlich schwer, sogar mit Hilfe von Computersimulationen. MIT Maschinenbau Forscher Khalid Jawed erklärte das Problem auf Gizmodo. "Wenn Sie einen Knoten und studieren die Form mit dem bloßen Auge, die Drehungen und Wendungen ziemlich kompliziert sind," Kräfte produzieren eine Mischung der Interaktion. Alle mathematisches Modell berücksichtigt die Drehungen und Wendungen, einschließlich der Variablen wie Spannung, Reibung und die Steifigkeit des Materials – seien es Schnürsenkel, Seil, Kopfhörer Kabel, Nylon, OP Faden oder sogar Falten, Proteine und DNA.

Bereits im Jahr 2008 dachte französischer Mathematiker Basil Audoly der Sorbonne Universitäten in Paris, er fand einen Weg, um genau das zu tun. Es funktionierte gut für sehr einfache Overhand Knoten mit nur ein oder zwei "turns", wie z. B. einen Dreiblatt-Knoten, gemacht durch eine Schleife machen und ein Ende des Seil oder Faden durch diese Schleife übergeben. Er dachte, es wäre eine einfache Sache, das Grundkonzept zu komplizierter Knoten mit mehr als zwei Umdrehungen zu verlängern.

Aber dann Jawed und seine Kollegen MIT beschlossen, Audoly Theorie zu testen und lief ein paar knotty Experimente ihrer eigenen, mit Nickel-Titan-Draht gespannt auf eine Tabelle im Labor. Sie verwendet einen mechanischen Arm, um den Knoten eng, Messung erforderliche Kraft, um die Schleife für Knoten mit einer wachsenden Zahl von Umdrehungen schließen ziehen. Überraschung! Sie fanden den Betrag der Kraft benötigt, um einen Knoten radikal verändert, da die Anzahl der erhöhten dreht.

Sie würden denken, dass mit jeder zusätzlichen Umdrehung, Sie nur ein bisschen mehr Kraft müssten auf den Knoten festziehen ausüben – eine lineare Verbindung zwischen der Anzahl der Drehungen und die Festigkeit des Knotens. Aber MIT Gruppe fand diese lineare Verbindung nicht halten. Wenn Sie eine Umdrehung, und dann Sie eine zweite Umdrehung machen, man würde müssen zwischen vier bis acht Mal mehr Kraft, um den Bund fürs Leben schließen – die Kraft erhöht eine quadratische oder gewürfelter gesetzlich vorgeschrieben. Dies erfordert ein komplexen Knoten mit zwei Umdrehungen 1000 Mal mehr Kraft, um den Kreislauf als einen Knoten mit einer einzigen Drehung zu schließen.

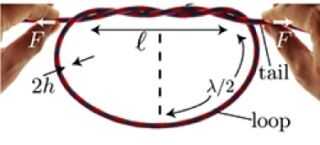
"Sie sehen können, diese auch mit die Drähte des Kopfhörers," sagte Jawed. "Sie machen ein drehen und ziehen, können Sie ganz einfach [schließen] den Bund fürs Leben, so dass die Größe der Schleife zu verringern wird. Aber wenn Sie fünf oder sechs Umdrehungen machen, wird es zunehmend schwieriger, es zu tun, und an einem gewissen Punkt nur kann man nicht mehr."

Aber warum ist dies geschehen? Kommt es zu Reibungen. Für einen einfachen Knoten mit nur ein oder zwei Kurven ist die dominierende Variable die Steifigkeit des Materials; Reibung ist also vernachlässigbar, es kann ignoriert werden. Aber als die Anzahl der Umdrehungen steigt um drei oder mehr, "Sie vergrößern die Kontaktfläche der verworrenen Region des Knotens, und das erzeugt viel Reibung" Jawed erklärt. So hatte das neue Modell Reibungskräfte sowie Steifigkeit und Topologie (Form) zu berücksichtigen.

Fasziniert von der MIT Gruppe finden, schlossen sich Audoly mit ihnen, um eine bessere Theorie zu entwickeln, die diese überraschende Versuchsergebnisse erklären konnte. Sie kamen mit einer Gleichung, die beschreibt, wie die verschiedenen Kräfte in einem Knoten funktionieren – Spannung, Reibung und Steifigkeit – beziehen sich auf die Anzahl der Windungen (der Knoten-Topologie).

Trotz seiner Vorhersagekraft ist dies nicht (noch) eine "Grand Unified Theorie der Knoten," anwendbar in allen Bereichen für jede mögliche Sorte. Es beschreibt nur die einfachste möglichen Knoten. Aber es ist ein ausgezeichneter Ausgangspunkt. Einfache Knoten sind die Bausteine, die kompliziertere Knoten bilden, und die Autoren sind optimistisch, dass sie ihre Herangehensweise an immer komplexere Knoten anhand von Computersimulationen erweitern können. Das wäre gut fürs Schneiderei bestimmte Konfigurationen von Knoten für verschiedene Anwendungen. Chirurgen, die Wunden nähen konnte die Stärke von ihren Knoten abhängig von der Anzahl der Windungen, die sie verwenden "tune". Es könnte auch zu einstellbaren Stoßdämpfer führen und zu einem besseren Verständnis der komplizierten entwirren der Fasern beteiligt Zellteilung.

"Eine Menge Wissen über Knoten empirische", sagte MIT Gruppenleiter Pedro Reis Wissenschaft. "Wir haben einen rationaleren Ansatz genommen und haben einen prädiktiven Rahmen geschaffen." "Es ist, was die Gemeinschaft fehlte."

Bild oben: Chirurg der Knoten in Nylon-Seil gebunden. Bildnachweis: Tom Murphy VI (via Wikipedia). Bild unten: Jawed Et Al./Physical Review Letters.

[Über Physical Review Letters und Wissenschaft]

Referenzen:

Audoly, B., Clauvelin, N., Neukirch, S. (2007) "elastische Knoten," Physical Review Letters 99:164301

Bayman, Benjamin F. (1977) "Theorie der Pannen," American Journal of Physics 45:185. [PDF]

Jawed, m.k. Et Al. (2015) "Entwirren der Mechanik und der Topologie in der Reibungs Antwort von langen overhand elastische Knoten" Physical Review Letters 115:118302.

Walker, Jearl. (1983) "in dem einfachen Gleichungen zeigen, ob ein Knoten wird halten oder Rutschen," Scientific American 249(2): 120